Séries não periódicas

O Diogo Lima me enviou por e-mail esse curioso sistema de amortização e pediu para desenvolver uma planilha de cálculo automático. O material que me enviou é do CursoBeta Online.
Na matemática financeira, é possível obter o valor presente (PV) de um empréstimo ou financiamento através da seguinte expressão matemática:

Colocando-se a prestação em evidência, teríamos:
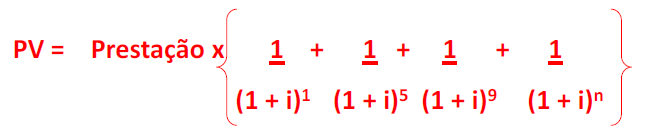
Os termos entre os colchetes são os fatores de atualização (ou de valor presente) a juros compostos, ou seja:

Logo:

Dessa maneira:

Ao analisarmos, o sistema francês de amortização, percebeu-se que o valor da prestação pode ser obtido através da expressão matemática abaixo:


No entanto, para que se possa utilizar tal expressão, os bancos deveriam cobrar os juros mensais sempre na proporção de 30 dias. Caso a cobrança dos juros seja realizada de forma pro-rata die, será necessário converter todos os fluxos para juros diários, trazer a valor presente com base em dias corridos e encontrar o coeficiente de financiamento para séries não periódicas através da seguinte expressão matemática:

Exemplo:
Determinado empréstimo obtido no dia 24/11/2017 de R$ 12.000,00 será pago em 12 parcelas com taxa de juros de 3% a.m. O banco calcula as prestações com base na série não periódica, ou seja, em dias corridos. A primeira parcela será paga 1 mês após a obtenção do empréstimo. Como encontrar o valor da parcela?
1º passo:
Contar quantos dias corridos entre uma parcela e outra:
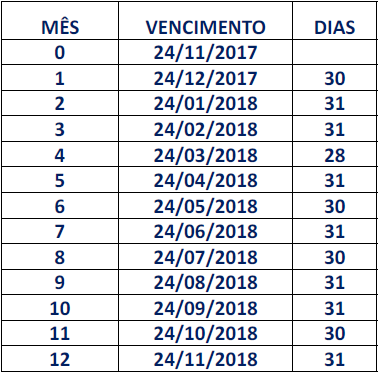
2º passo:
Contar quantos dias acumulados entre cada parcela e a data do empréstimo:

3º passo:
Calcular o fator de atualização de cada parcela como base nos dias corridos:

Como encontrar o fator?
Mês 1 por exemplo 1 / [(1 + 0,03)30/30] = 0,970874
Mês 2 por exemplo 1 / [(1 + 0,03)61/30] = 0,941668
E por aí vai!!!
4º passo:
Calcular os juros mensais com base nos dias corridos (Ou seja, se forem 30 dias será 3%, se forem 31 dias será maior):

Como encontrar a taxa de juros?
Mês 1 por exemplo [(1 + 0,03)30/30] – 1 = 0,03 (3%)
Mês 2 por exemplo [(1 + 0,03)31/30] – 1 = 0,031015 (3,10%)
E por aí vai!!!
5º passo:
Somar todos os fatores e achar o coeficiente de financiamento (1 / soma dos fatores):

6º passo:
Calcular a prestação:
Prestação = 12.000,00 x 0,100654579 (1.207,85)
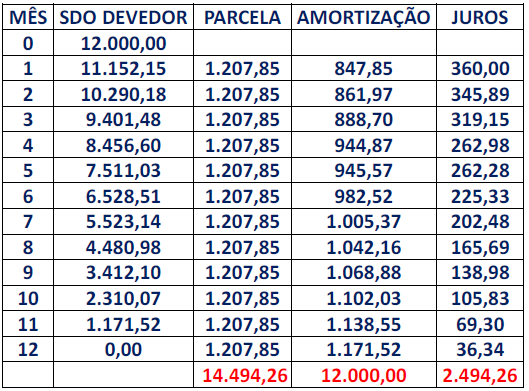
Caso a empresa calculasse sempre com base em 30 dias:
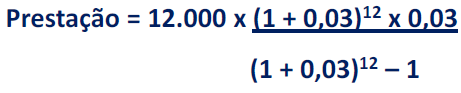
Prestação = 12.0000 x 0,100462 -> Prestação = 1.205,55

IMPORTANTE:
Os juros de acerto e as séries não periódicas são os principais motivos de diferenças entre os cálculos de diversos peritos e os cálculos das instituições financeiras. FIQUE ATENTO!!!
A planilha com os cálculos automáticos estão no pacote de planilhas chamado “Sistemas de amortização”, basta clicar no link para ser direcionado.


Boa tarde!
O Sr. tem modelo de tabela não periódica que eu possa adquirir?
Estou começando trabalhar com perícia.
Favor enviar Chave Pix, posso pagar antecipado.
Olá Ivan, tem sim, basta você acessar o site oficial simor.tech
Jorge, boa tarde!! Tentei aplicar a sua fórmula e não deu certo. Fiz e refiz no papel e no excel. O meu primeiro pagamento/intervalo é 60 dias após o início, e não trinta. Será que é isso?
Olá Pedro, creio que é isso sim, no site simor.tech tem a planilha para compra. Se for o caso também você poderá me enviar a planilha por e-mail para eu dar uma olhada.
Jorge, fiz a compra e deu certo. Mas não entendi como. Vou estudar a planilha e descobrir. Obrigado.
Jorge, parabéns pela página. Bem didático seu texto, ajudou bastante! Obrigado!
Fico feliz em ajudar!